En este tutorial se mostrarán las operaciones básicas con matrices, tomando en cuenta que ya se conocen todos los conceptos básicos, como, qué es una matriz, operaciones con matrices, qué es una fila, columna o renglón, entre otros, sólo se explicará cómo utilizar MATLAB para el manejo de matrices.

En MATLAB las matrices se crean utilizando corchetes, los valores de un renglón se separan por comas, para pasar a otra fila, se utiliza punto y coma (;).
Por ejemplo, para una matriz de 2X2, se utiliza la siguiente sintaxis: A=[R11, R12; R21, R22]

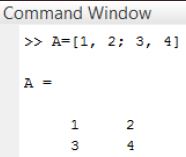
Al presionar enter, el programa mostrará la matriz creada en la variable A. Se utiliza la letra R para definir el valor del renglón y la posición de cada valor. Por ejemplo, si queremos que los valores sean 1 y 2 para el primer renglón, y, 3 y 4 para el segundo renglón, se escribe como: A=[1, 2; 3, 4]
Obteniendo lo siguiente:

También es posible comenzar otro renglón presionando enter en lugar de utilizar punto y coma, depende de las necesidades de cada persona.
Si ya se tiene una matriz y se quiere conocer su dimensión, se utiliza el comando size, por ejemplo: size(A) donde al presionar enter, nos dará la dimensión de la matriz, en este caso, el resultado será 2 2, ya que la matriz que creamos anteriormente es de 2X2.

Para conocer la longitud de un vector o número de líneas o renglones de una matriz, se utiliza el comando length, con la misma sintaxis: length(A).

Para generar una matriz identidad, existe el comando eye, cuya sintaxis es: eye(d), donde d es la dimensión de la matriz, por ejemplo, para una matriz identidad de 3X3:

El comando max determina el componente máximo en un vector, o determina el vector fila con los componentes de mayor valor en cada columna de una matriz.

Por ejemplo, se tiene la matriz A=[2,1,0;5,3,1;10,7,9]
Al escribir max(A) obtendremos el valor más grande de cada columna.

Si se requieren los valores contrarios, es decir, los valores mínimos, se utiliza el comando min.

Con el comando median se genera un vector fila cuyos componentes son el promedio en cada columna de la matriz. Para la matriz A, se escribe: median(A).

El comando std sirve para generar un vector fila que contiene la desviación estándar de cada una de sus columnas: std(A).

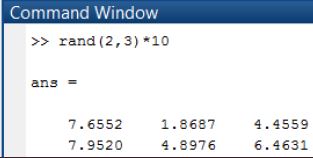
El comando rand permite crear una matriz con valores aleatorios, la sintaxis es: rand(m,n), donde m son las filas y n los renglones, también se puede utilizar rand(n) para una matriz cuadrada.

Este comando por lo general crea números decimales, por lo que se le puede agregar alguna operación para alterar el resultado, por ejemplo, multiplicar la matriz por 10 para obtener números más grandes.

El comando magic permite crear una matriz mágica de orden n, en la que las filas y las columnas suman la misma cantidad, con entradas enteras. La sintaxis es: magic(n).

El comando ones genera una matriz unitaria de orden n, la sintaxis es ones(n).
Por el contrario, el comando zeros genera una matriz de ceros de orden n, la sintaxis es la misma.

Los comandos triu y tril generan una matriz triangular, debajo y encima de la diagonal respectivamente. La sintaxis es triu(X) y tril(X) donde X es la matriz.
El comando diag arroja los valores de la diagonal de una matriz, la sintaxis es diag(X) donde X es la matriz, por ejemplo:

Operaciones básicas

Para suma, resta, multiplicación y división entre una o más matrices, éstas deben ser de la misma dimensión, no es posible sumar una matriz de 3X3 con una de 3X2.

Por otro lado, sí es posible sumar un número a una matriz, ya que ese número se suma a cada valor de la matriz. Esto puede ser por ejemplo: A+2, esta operación suma 2 a cada elemento de la matriz A.

Pero si se requiere hacer A+B, ambas matrices deben ser de la misma dimensión.

El comando inv devuelve la matriz inversa, su sintaxis es inv(X), donde X es la matriz a utilizar.

Para obtener la determinante de una matriz, se usa el comando det, la sintaxis es: det(X), donde X es la matriz.

Un ejemplo de un programa en MATLAB para el uso de estas funciones es el siguiente:

%Ejemplos con matrices
disp(‘Se creó una matriz aleatoria de 3X3’);
A=rand(3);
A
disp(‘Se obtendrá la determinante de la matriz A’);
disp(‘Presione una tecla para continuar’);
pause;
D=det(A);
D
disp(‘Ahora se obtendrá la inversa de la matriz A’)
disp(‘Presione una tecla para continuar’);
pause;
I=inv(A);
I
disp(‘Se multiplicará la matriz A por la inversa de A’);
disp(‘Presione una tecla para continuar’);
pause;
M=(A*I);
M