Otro método para resolver convoluciones es el de Malla, parecido al de suma por columnas, pero en este caso, utilizando una tabla para hacer las operaciones.
Utilizando el sistema anterior:
x[n] = {1, -1, 1}
h[n] = {2, 1}
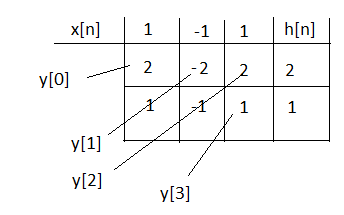
La tabla se arma como se ve en la figura:
Se multiplica el renglón de x[n] por cada elemento de la fila h[n], luego, los resultados se suman en diagonal para obtener los valores de y[n], como se observa, y[0] vale 2 porque no hay otro valor para sumarle, al igual que y[3].
De esta manera, queda expresado como:
y[0] = 2+0 = 2
y[1] = -2 + 1 = -1
y[2] = 2+(-1) = 1
y[3] = 1+0 = 0
y[n] = {2, -1, 1, 1}