En este tutorial crearemos un programa en LabVIEW que realice los cálculos necesarios para comprobar la Ley de Enfriamiento de Newton, a partir de valores conocidos dados.
Marco teórico
Se denomina enfriamiento newtoniano al proceso de enfriamiento que sigue una ley experimentalmente determinada por Isaac Newton, en la que la velocidad de enfriamiento de un cuerpo cálido en un ambiente más frío Tm, cuya temperatura es T, es proporcional a la diferencia entre la temperatura instantánea del cuerpo y la del ambiente.

La expresión de la ecuación #1 no es del todo precisa y se considera una aproximación válida para pequeñas diferencias entre T y Tm. En todo caso, la expresión es útil para mostrar cómo el enfriamiento de un cuerpo sigue aproximadamente una ley de decaimiento exponencial:
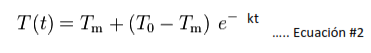
Una formulación más precisa sobre el enfriamiento de un cuerpo en un medio requeriría un análisis del flujo de calor del cuerpo cálido en un medio heterogéneo de temperatura. La aplicabilidad de esta ley simplificada se determina por el valor del número de Biot.
Tutorial
Ecuaciones utilizadas para el desarrollo del programa

Dónde:
- K es la constante de proporcionalidad
- T es la temperatura del objeto (en grados centígrados)
- Tm es la temperatura del medio en la que se encuentra el objeto (en grados centígrados)
- t es el tiempo en que se enfría o calienta el objeto (en segundos)
Ecuación para determinar la temperatura de un objeto en un tiempo determinado:

Ecuación para encontrar la temperatura del medio ambiente donde está el objeto a analizar:

Ecuación para obtener la constante de integración C:

Ecuación para obtener la constante de proporcionalidad K:

Ecuación para encontrar el tiempo transcurrido ante una temperatura determinada:

El panel frontal del prototipo del programa en LabVIEW queda de la siguiente forma:

Para que el programa funcione, es necesario conocer los cuatro datos de entrada: temperatura inicial, tiempo final, temperatura después de un tiempo determinado y temperatura ambiente (Ti, Tf, tf, Tm).
Con estos datos, el programa calcula la constante de integración C y la constante de proporcionalidad K.
Con un control de temperatura, el usuario puede variar la temperatura o el tiempo según se requiera.
El diagrama de bloques queda de la siguiente manera:

Al ejecutar el programa, es necesario activar los botones en la sección «Datos que se conocen», para tener en cuenta que se tienen los datos necesarios para poder realizar el cálculo.
Los datos conocidos, se ingresan en los controladores numéricos, una vez ingresados los 4 valores, se obtiene la constante de integración C y la constante de proporcionalidad K.
Para hacer el cálculo de la constante de integración, se calcula el logaritmo natural de la variable r (variable correspondiente de la función nodo de fórmula que toma el valor de una operación antes realizada). Mismo caso para obtener el tiempo, calculando el logaritmo natural de la variable o, correspondiente a una operación anterior.
Con una gráfica, se observa el comportamiento de la temperatura respecto al tiempo transcurrido en segundos. Se puede exportar una tabla de Excel con los datos obtenidos.
Para enviar los datos a la gráfica, se toman los valores del tiempo de la temperatura y con un build array, se obtiene una salida tipo Array 2D, que se enviará al indicador de la gráfica.
En el caso de los botones de información, se utiliza la función «Display Message to User», que se habilita con un botón.
Prueba del programa
Se tiene el siguiente cuestionamiento como prueba:
La temperatura de una taza de café acabada de servir es de 200 °C. Un minuto después, se ha enfriado a una temperatura de 190 °C en una habitación que se encuentra a una temperatura ambiente de 70°C. ¿Cuál es el tiempo que debe transcurrir para que el café alcance una temperatura de 150 °C?
Para obtener la constante de integración, se desarrolla la siguiente integral:

Al desarrollar la integral, se obtiene la diferencial de T, después se obtiene el logaritmo natural a la sustracción de T y 70, dejando la constante de integración como incógnita, que al despejar, se obtiene el resultado, en este caso, C = 130.
Después, se sustituyen los valores proporcionados en el programa, mediante las ecuaciones proporcionadas.


Se puede observar los resultados en el programa:

Se observa una ligera variación en los decimales del resultado final debido a que el programa no toma en cuenta la misma cantidad de decimales que en los cálculos realizados a mano.
Al exportar los datos de la gráfica en Excel, se puede obtener algo como lo siguiente:

Se obtienen muchas lecturas iguales debido a que la gráfica se actualiza cada 500 ms, valor que puede modificarse en el código del programa dentro del ciclo while.
Puedes descargar el VI para ver su funcionamiento aquí.
Si requieres algún programa en específico, no dudes en contactarnos aquí para una cotización.